Volume Of A Sphere With Diameter 21

A solid metallic sphere of diameter 21 cm is melted and recasted into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed. A cylindrical can of internal diameter 21 cm contains water.

A solid sphere whose diameter is 10.5 cm is lowered into the cylindrical can. The sphere is completely immersed in water. Calculate the rise in water level, assuming that no water overflows. Report "A solid metallic sphere of diameter 21 cm is melted and recasted into a number o..." A solid metallic sphere of diameter 21 cm is melted and recasted into a number o...

If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. A hollow sphere of internal and external radius 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm.

Find the height and slant height of the cone. A hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. The core, assembled, was designed to be at "−5 cents".

So far we've calculated the volume of cubes, rectangular tanks, and cylinders. Using that information, how do you think we would calculate the volume of a sphere? What variables do you think you would use? Take a few moments to think about it before we go through the explanation below.

A cylindrical can of given internal diameter contains water. A solid sphere whose diameter is given is lowered into the cylindrical can. The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of height 2 \(\frac \) cm.

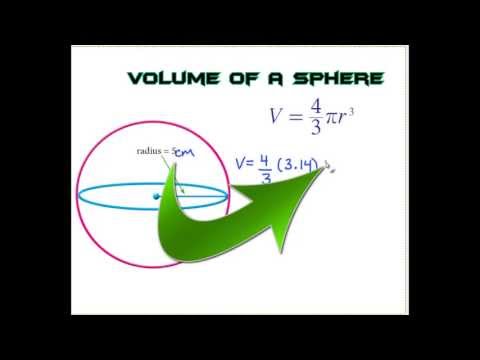
Find the diameter of the cylinder. If it is melted and recast into a solid cylinder of height 22/3 cm. In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches.

A sphere is a 3-dimensional round object. The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. Simply enter the desired value in the relevant box. Please use only numbers (e.g. enter 22 not 22 cm).

This calculator only uses numbers. If you try to enter a unit of measure (e.g. 22 metres, 4 miles, 10 cm) you will get an NAN error appear in each box. When you have entered the number that you know, click the button on the right of that box to calculate all the other values. For example, if you know the volume of a sphere enter the value into the bottom box and then click the calculate button at bottom right. The pi in the formula is the constant that we use when finding the circumference of a circle, and the radius, as you might remember, is half the length of the diameter. The last thing is that the radius is cubed.

This relates to the fact that in the end we are solving for volume, which has three dimensions. If the density of metal is 8.4 gm/dm3, calculate the mass of a metallic sphere of radius 0.5 dm. A metallic sphere of radius 10.5 cm is melted and thus recast into small cones each of radius 3.5 cm and height 3 cm. A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder.

The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.

A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface.

The formulas for the volume and surface area of a sphere are given below. As the reflectors were manually moved closer and farther away from each other, scintillation counters measured the relative activity from the core. The experimenter needed to maintain a slight separation between the reflector halves in order to stay below criticality.

Our tutors have indicated that to solve this problem you will need to apply the Density of Geometric Objects concept. The surface area of a solid metallic sphere is 616 cm2. There is surface area and volume of sphere equal, find the radius of sphere. In this calculation you can calculate the volume of a sphere with a number of given input values, such as radius, diameter, circumference.

You also have a number of different input units and can choose output unit according to your likings. Q9.Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the radius r' of the sphere, ratio of S and S'. Q6.The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white washing its curved surface at the rate of Rs. 210 per 100 m2. A tomb is in the form of a cylinder surmounted by a hemisphere.

The radius and height of the cylindrical portion are 10.5 m and 9 m. The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. If a hollow sphere of intefnal and external diameters 4 cm and 8 cm respectively melted into a cone of base diameter 8 cm, then find the height of the cone.

A sphere, a cylinder and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. A cone and a hemisphere have equal bases and equal volumes.

A cylinder whose height is two thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder. A sphere of radius 5 cm is immersed in water filled in a cylinder, the level of water rises \(\frac \) cm. A sphere, a cylinder, and a cone have the same diameter.

Q. Consider equal volumes of a given substance in solid, liquid and gas phases. Arrange them in order of decreasing mass based on the trend... Unlimited random practice problems and answers with built-in Step-by-step solutions. Practice online or make a printable study sheet. Consider a sphere and two right circular cones of same base radius and height such that twice the radius of the sphere is equal to the height of the cones.

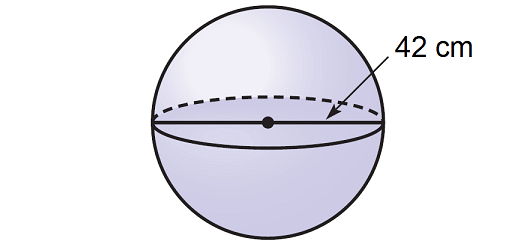
Find the volume and surface area of a sphere of diameter 42cm. Q8.A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl. Q7.A joker's cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.

The volume of sphere varies directly as the cube of its radius and the volume of sphere is 36π cubic centimetre.find the volume of sphere, when the diameter is doubled. Find the volume and surface area of a sphere of radius 2.1 cm. A hollow sphere of internal and external diameter 4 cm and 8 cm respectively, is melted into a cone of base diameter 8 cm. If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.

A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at ₹7 per 100 cm2. A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved surface area of the shape if the length of the shape be 7 cm.

The curved surface area of a cylinder is 1320 cm2 and its base had diameter 21 cm. Find the height and volume of the cylinder. A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters. Round the answer to the nearest hundredth. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center.

The volume of a sphere is measured in cubic units. A thin cardboard sheet is used to cover the curved surface area of a cylinder with radius 10.5 cm and height 30 cm. Find the area of the cardboard sheet used. The surface area of a solid sphere is the same in square cm as its volume in cubic cm. Find the volume and surface area of a sphere of diameter 14 cm. Find the volume and surface area of the sphere of radius 21 cm.

Find the volume and surface area of a sphere of radius 21 cm. Find the volume and surface area of a sphere of diameter 21 cm. The total surface area of a hollow metal cylinder, open at both ends of external radius 8 cm and height 10 cm is 338π cm2. Consider a right circular cylinder and three right circular cones of same base radius and height as that of the cylinder. I'm a retired math teacher, but it's been so many years since I used this I had forgotten the formula. I wanted to know how much the volume increased when the radius doubled.

Now I know--it's eight times because the two is cubed. To calculate the volume of the full sphere, use the basic calculator. Q2.The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in Fig. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm' and black paint costs 5 paise per cm2.

Q8.A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas. Q2.Find the total surfce area of a cone, if its slant height is 21 m and diameter of its base is 24 m. Q1.Diameter of the be of a cone is 10.5 cm and its slant height is 10 cm. Q1.The curved surface area of a right circular cylinder of height 14 cm is the diameter of the base of the cylinder.

The question becomes, "Where does the 4/3 come from? " Well the explanation for that is actually quite a long one, and I'll leave that for another day. Using a bit of mathematical wizardry the 4/3 ends up being derived from this fact. Find the height of a cone of radius 30 cm which is formed by melting a sphere of radius 30 cm. Volume of solid, hollow sphere and hemisphere. Find the total surface afea of a hemisphere of radius 10 cm.

A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1m, then find the volume of the iron used to make the tank. The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the figure. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2. If the inner radius is 1 m, then find the volume of the iron used to make the tank. A cone and a hemisphere have equal bases and volumes.

Showing where these formulas come from, like we did for a rectangular solid, is beyond the scope of this course. We will approximate \pi [/latex] with 3.14[/latex]. The surface area of a solid sphere is 1254 square feet. Find the volume of the solid sphere.